Gunden Geri Kalanlar

Yaklasik iki haftalik aranin ardindan, Cern’deki grubun islerini anlattigim ATLAS Week toplantisindan sonra, tekrar sahalara donmenin heyecanini yasiyorum. Kaldigimiz yerden devam edelim.

Coursera’daki Accelerated Computer Science kurs serisinin, ucuncu ve son dersine basladim bu hafta: Underordered Data Structures. Gecen dersteki array, linked-list, tree gibi “ordered” veri yapilarindan yavas yavas hash table, graph gibi “unordered” veri yapilarina geciyoruz. Ilk hafta hash table konusu ile biraz beyin yakan kivamda basladi.
- Hash table’lar elimizdeki key - value seklinde ikilileri efficient bir sekilde saklamamizi sagliyor. Daha dogrusu elimizdeki bir veriyi, belirli bir key ile kaydedip, sonrasinda buna hizli bir sekilde (sabit zamanda) erisebilmemize olanak sagliyor.
- Bunu saglamak icin, veri ile iliskili key degerini, veriyi tutacagimiz array‘i duzgun bir sekilde indekslemesi icin “hash” etmemiz gerekiyor. Bunun icin hash function kullaniyoruz. Bu fonkiyon iki sey yapiyor. Birincisi key degerini alip bir sayisal degere ceviriyor (hashing); sonrasinda bu degeri alip veriyi tutacagimiz array’in boyutlarina gore sinirlandiriyor (compression). Iyi bir hash function h(x) sunlari saglamak durumunda:
  - Verilen bir key‘i sabit bir zamanda islemeli.
  - Deterministik olmali
  - Simple Universal Hashing Assumption (SUHA)‘i saglamali
- Tum bunlari saglayan bir fonksiyon belirledikten sonra dikkat etmemiz gereken bir de collision konusu var. Yani verilen bir key degerini hash ettigimizde cikan indeks baska bir key icin verilmisse ne yapacagiz? Bunun icin uc yontem var:
  - Seperate Chaining - collision olan *key*leri birbirine linked-list seklinde baglamak.
  - Linear Probing - collision durumunda, hesaplanan indeksten baslayip tek tek ilerleyerek bos olan indekse yerlestirmek
  - Double hashing - collision durumunda, ikinci farkli bir hash function daha kullanarak yeni indeks hesaplamak
  Her birinin farkli avantajlari ve dezavantajlari var. Ornegin seperate chaining ile, ekleyecegimiz key‘i O(1) zamanda, tak diye yerlestirebiliyoruz fakat Linear Probing ile ust uste collision durumlarinda, hep bir sonraki bosluklari doldurarak array‘de belirli cluster‘lar olusturuyoruz. Boylece veriyi array‘e uniform bir sekilde dagitmamis oluyoruz.
- Gunun sonunda boyle bir veri yapisinda, istedigimiz veriye ne kadar hizli ulasacagimizi belirleyen kritik bir parametre var: load factor (alpha). Hash edecegimiz key sayisi (n) ile bunlari tutacagimiz array‘in buyuklugunun (N) oranina karsilik geliyor: n/N. Bu oran ne kadar dusukse hashing operasyonu o kadar hizli calisacak demektir. Bu orani dusuk tutmanin yollarindan biri de array‘i duzenli bir sekilde buyutmek. Belirli bir kritik degerde tuttugumuz surece (alpha = 0.6), hash-table‘i efficient bir sekilde kullanabiliyoruz - O(n/N) sabit zamanda.
- Fakat elimizdeki veri buyuk objelerden olusuyorsa ornegin, bunlari bir array icinde birbiri ardina saklamak iyi bir fikir olmayabilir. Bunun yerine linked-list daha makul. Yada elimizdeki veriyi belirli bir sebepten oturu, komsuluk iliskisini koruyarak tutmak istiyoruz diyelim; hash-table’lar bu durumlar icin de iyi bir fikir degil. Bunun yerine tree-based yapilar (ronegin AVL tree) daha iyi bir secenek olacaktir.
- Python’daki dict yapilarinin altinda yatan veri yapisi hash-table. Bir cok iste beni kurtaran bir yapi olmasi sebebiyle epey sIk kullaniyorum kendi islerimde de. Altta yatan fikri, kabaca da olsa anlamak benim icin epey guzel oldu. Konuyla ilgili gecen gunler okudugum su temel yaziyi da ekleyim: Hash-tables
Colombia Unv.‘den Applied Machine Learning dersine “Linear Models” dersi ile devam. Dersi anlatan kisinin scikit-learn kutuphanesinin core gelistiricilerindan (Andreas Muller) olmasi sebebiyle derste gerek kutuphaneye dair muthis trickler, gerekse de yontemlerin altindaki mekanizmalara dair ilginc nuanslar ogreniyorum. Bu derste konu, ilk basta veri icinde eksik degerler, missing-value, icin cesitli cozumler, sonrasinda da linear modeller uzerineydi. Ilgili dersin slaytlari ve aciklamalari surada.
- Missing-value problem
  - Icinde missing value barindiran bir satiri veriden silerken, ayrica boyle bir durumun production‘da karsimiza ciktiginda nasil hareket edecegimizi her zaman dusunmemiz gerekiyor.
  - scikit-learn’de ilgili degeri o kolonun ortalamasi, medyani ya da bizim belirledigimiz sabit bir degerle degistirebilmemizi saglayan bir transformer var: SimpleImputer.
```
  from sklearn.impute import SimpleImputer
  imp = SimpleImputer(strategy="median").fit(X_train)
  X_median = imp.transform(X_train)
```
  - Transformer ozelliginden dolayi, bunu ayni zamanda pipeline’a da ekleyebiliriyoruz.
```
  from sklearn.pipeline import make_pipeline
  from sklearn.preprocessing import StandardScaler
  from sklearn.linear_model import LogisticRegression

  pipe = make_pipeline(imp, StandardScaler(), LogisticRegression())
```
  - SimpleImputer‘in bir adim otesi, eksik olan veriyi doldurmak icin diger verileri kullanarak bir model olusturmak. Ornegin arka tarafta k-Nearest Neighbor ya da RandomForest kullanip, eksik veri tahmin edilebilir. Her eksik veriye sabit bir deger atamaktan cok daha saglikli bir yontem bu, fakat haliyle “overhead”i yuksek. Bunun icin de hazir KNNImputer fonksiyonu kullanilabilir:
```
  knn_pipe = make_pipeline(KNNImputer(), StandardScaler(), LogisticRegression())
```
  Ya da, IterativeImputer kullanilarak istedigimiz modeli verebiliriz:
```
  rf_imputer = IterativeImputer(precitor = RandomForestRegressor())
  rf_pipe = make_pipeline(rf_imputer, StandardScaler(), LogisticRegression())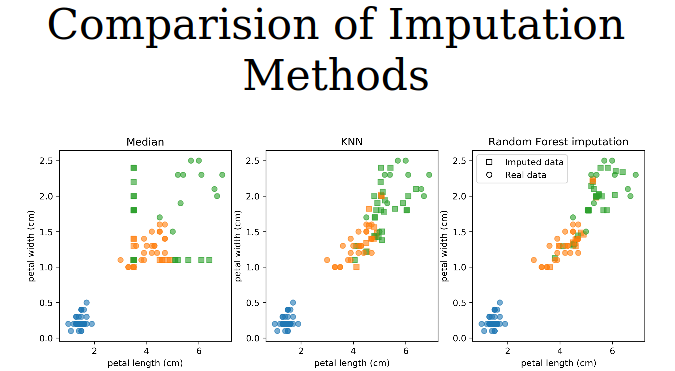
```
  Kaynak: A. Muller
- Linear model olarak ilk akla gelen Ordinary Least Squares. Bu modelin tek (unique) cozumu oldugu durum, veri matrisimizin full-column rank‘e sahip oldugu durum. Bu durum satir sayimizin, sutun (feature) sayimizdan cok daha fazla oldugunda ancak kolaylikla saglanan bir durum. Aksi durumda, yani feature sayisinin satir sayisindan fazla oldugu durumda regularisation yontemleri uygulayarak unique cozumu elde edebiliyoruz.
- Regularisation ile, loss fonksiyonuna model parametrelerinin buyukluklerini kisitlayan yeni bir terim ekliyoruz ve optimizasyon sirasinda hem loss fonksiyonu hem de regularisation terimini minimize eden bir cozum ariyoruz. Regularisation terimini kontrol etmek icin de alpha parametresini kullaniyoruz. Bu konuda iki secenegimiz var: l1 (Lasso) ve *l2 (Ridge).
  - l1 regularisation‘da loss function‘a ekledigimiz terim, parametrelerin mutlak buyukluklerinin toplami. Boylece son elde edilen model bircok parametrenin buyuklugunu sifira indiriyor; daha basit bir model elde ediyoruz. Bu yontemi onemli degiskenleri secmek icin de bir nevi feature selection amacli olarak da kullanabiliriz. Bu noktada dikkat edilmesi gereken, parametresi 0 olan degisken, onemsiz degisken olmayabilir, daha cok icinde barindirdigi bilgi diger degiskenler tarafindan karsilaniyor demek daha dogru.
  - l2 regularisation‘da ise loss function‘a parametrelerin karelerinin toplamini ekliyoruz. Bu sayede bircok terimi sifira yaklastiriyor ve geri kalanlar bir grup parametre ile train ve test verisini aciklayabilecek bir model elde ediyoruz. Bu yontem, buyuk terimleri digerlerine gore daha fazla penalize ediyor.
  Her ikisi icin de regularisation’in ne kadar etki edecegini belirleyen alpha parametresini gridCV ile aramamiz gerekiyor. Sonucta, alpha’yi degistirdikce train-test sonuclarinin degistigini ve ozellikle sifirdan farkli olan parametre sayisinin gittikce azaldigini, modelin karmasikliginin azaldigini goruyoruz.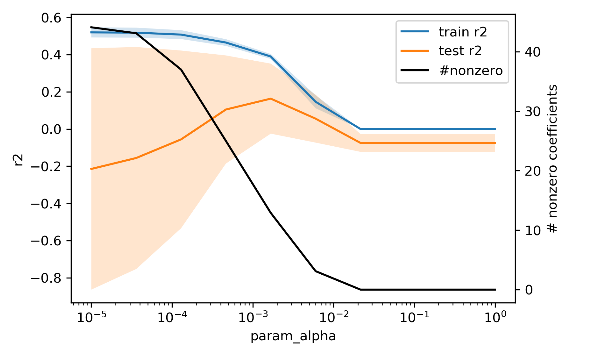
  Kaynak: A. Muller
- Bir de l1 ve l2‘yu bir araya getiren, her iki terimi de ekleyip optimize eden Elastic-Net modeli mevcut. Hangisinin daha etkili olacagini belirtmek icin de scikit-learn’de l1-ratio parametresi tune edilebiliyor.
```
from sklearn.linear_model import ElasticNet
param_grid = {'alpha': np.logspace(-4, -1, 10),
              'l1_ratio': [0.01, .1, .5, .8, .9, .95, .98, 1]}
grid = GridSearchCV(ElasticNet(), param_grid, cv=10)
grid.fit(X_train, y_train)
```