Haftaya veri yapilariyla acilis yaptik. Bu hafta ve onumuzdeki hafta iki buyuk toplantida genis capli iki sunumum oldugundan muhtemelen, daha kompakt bir icerik olacak. Her gun not tutma aliskanligini epey ilerlettim, kisa da olsa buradan paylasmaya devam edecegim.
Bu hafta Accelerated Computer Science dersi,
Treealgoritmalarinin “son noktasi”, bir priority queue veri yapisi tasarlamak uzerineydi. Bu veri yapisi, Binary Search Tree’den daha “strict” on kosullara sahip olsa da, veriyi tutma sekliyle, minimum elemanina sabit zamanda ulasabilme imkani veriyor.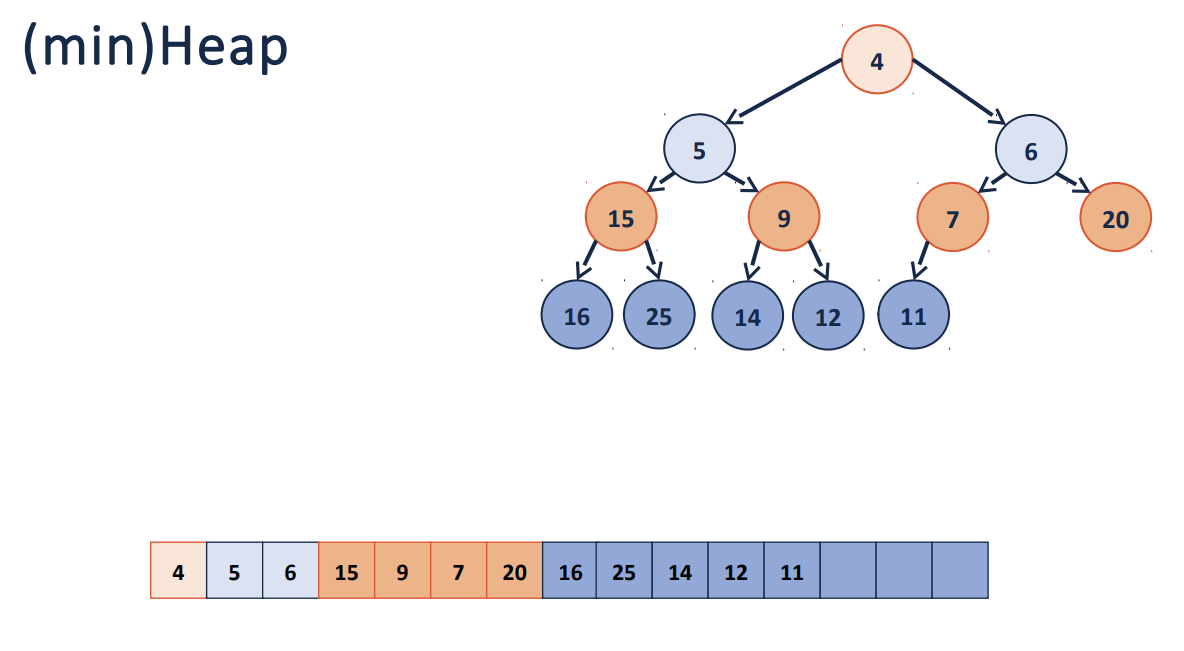
Kaynak: Coursera Accelerated Computer Science Tanim olarak Binary-tree minimum heap, her bir node degerinin kendi parent node’un degerinden daha buyuk oldugu tree’ler olarak tanimlaniyor. Boyle bir yapiyi kosul olarak koydugumuzda, akillica bir indeksleme kullanarak bu yapiyi karmasik bir
Treeyerine, basit birarrayile tutabiliyoruz.Heap’e yeni bir veri ekledigimizde, Tree’nin heap ozelligini korumamiz gerekiyor (buna gore cesitli
swapislemleri yapmak gerek). Ayrica Tree dolu oldugunda uygun bir sekilde buyutmek gerekiyor (buyuklugunu iki katina cikararak).Heap’ten minimum degeri cikardigimizda da ayni yapiyi korumak icin, Tree’nin en sagindaki degeri root’a tasiyip, sonra gerekli swap islemleriyle tekrar heap yapisini koruyoruz.
Heap’lerin guzel tarafi bize verilen herhangi bir
string,listgibi (siralanmamis) bir yapiyi alip rastgele bir Tree olusturup, alttan yukari dogru swap ede ede, her bir node’un parent node’dan buyuk oldugu sekle O(n) zamanda getirebiliyoruz. Sonrasinda O(log n) zamanda da minimum elemani heap’ten cikarabiliyoruz.Heap yapisinin kullanildigi onemli bir yer ise heap-sort algoritmasi. Elimizdeki bir koleksiyonu, oncelikle O(n) zamanda bir heap’e donusturuyoruz; sonrasinda n kere, her biri O( log n) zamanda minimum elemani heap’ten cikarip diziyoruz. Boylece toplamda O(n log n) zamanda calisan bir siralama algoritmasi elde etmis olduk!
Bugunku LeetCode Challange calistigim yerden cikti! Basit bir Binary Search Tree‘de verilen bir degeri arama problemi; gozum kapali cozdum!
# LeedCode June Challange Day 15
# Binary Search Tree Problem
# Given the root node of a binary search tree (BST) and a value.
# You need to find the node in the BST that the node's value equals the given value.
# Return the subtree rooted with that node.
# If such node doesn't exist, you should return NULL.
# For example,
# Given the tree:
# 4
# / \
# 2 7
# / \
# 1 3
# And the value to search: 2
# You should return this subtree:
# 2
# / \
# 1 3
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
while(root != None):
if(val == root.val):
return root
if(val < root.val):
return searchBST(root.left, val)
elif(val > root.val):
return searchBST(root.right, val)
return None
Bugun Python konusunda okudugum en ilginc iceriklerden biri Real Python’daki “SimPy: Simulating Real-World Processes With Python” tutorial’iydi. Gunluk hayattaki is sureclerini modelleyip, belirli sinirli kaynaklarla en iyi cozumu gelistirmek icin cesitli simulasyonlar yapmayi saglayan bir modul
simpy. Problemi modulun sagladigi komponentlerle tum detaylariyla tanimlayip, sonrasinda koydugumuz kisitlari Monte Carlo vari bir simulasyonla senaryoyu bircok kez calistirip, elde ettigimiz sonuclarin istatistiklerini inceliyoruz. Tutorial’da bir sinema gisesinde kisilerin bilet alimindan salonda kotuklarina oturmalarina kadar gecen surenin en fazla 10 dakika olacak sekilde bir senaryo icin kac gise gorevlisi gerektigi problemi cozuluyor. Boyle bir kutuphane oldugunu ogrendigim iyi oldu; ilerleyen zamanlarda kafamdaki simulasyon fikirleri icin mutlaka geri donecegim gibi duruyor.Bir baska guzel Python yazisi ise, calistirdigimiz bir programin hangi kisminin cok fazla hafiza (memory) tukettigini profile etmenin kullanisli bir yolunu anlatan bir yazi: Debugging out-of-memory crashes in Python. Bunun icin kullandigi
filprofilerpaketi.